模型训练核心技巧：学习率预热、余弦衰减与梯度裁剪

本篇我们来深入探讨一下学习率预热（Learning Rate Warmup）、余弦衰减（Cosine Annealing）和梯度裁剪（Gradient Clipping）这三种在深度学习训练中非常实用的优化技巧。

首先，这三个技巧的核心目标是一致的：让模型在复杂的高维损失函数空间中，更稳定、更高效地找到一个好的解（局部最优解或全局最优解）。

它们分别从不同角度解决了训练过程中可能遇到的问题：

学习率预热 (Warmup)：解决训练初期的不稳定性。
余弦衰减 (Cosine Annealing)：解决训练中后期的精细调整和收敛问题。
梯度裁剪 (Gradient Clipping)：解决训练过程中可能出现的梯度爆炸问题，充当“安全带”。

接下来我们逐一解析。

学习率预热 (Learning Rate Warmup)

结论先行

在训练开始的几个周期（epoch）或迭代（step）内，将学习率（Learning Rate）从一个非常小的值（例如 0）线性或非线性地增加到预设的初始学习率。预热阶段结束后，再采用预设的学习率衰减策略（如余弦衰减）。

本质是什么

在训练之初，模型的权重是随机初始化的，可以说它对数据一无所知。如果此时直接用一个较大的学习率（Learning Rate），就好比让一个新手司机上来就踩满油门，结果很可能是车辆失控（模型参数被带到很差的空间），导致训练初期的剧烈震荡，甚至无法收敛。

学习率预热就是为了解决这个问题。它在训练开始的几个周期（epoch）或迭代（step）内，将学习率从一个非常小的值（甚至是 0）逐步提升到你预设的初始学习率。

它的本质是 在模型尚未稳定时，通过控制更新步长来增加训练的稳定性。

这是一种 "先慢后快" 的策略。它承认了模型在训练初期处于一个非常不稳定的状态，因此需要一个缓冲期。通过这个缓冲期，模型可以安全地度过最不稳定的阶段，为后续高效的训练打下坚实的基础。

好处有哪些

防止模型在训练初期"震荡"或"发散"：在训练刚开始时，模型的权重是随机初始化的，它们距离最优解非常遥远。此时如果直接使用一个较大的学习率，梯度更新的步子会迈得很大。这就像在一张崎岖不平的地图上蒙眼寻宝，一开始就猛冲一步，很可能会直接冲进一个很差的区域（损失函数的“悬崖”），导致损失剧增，模型难以收敛。
给模型时间适应数据：在训练初期，模型对数据还没有任何认知。一个较小的学习率可以让模型"温柔"地开始学习，逐渐适应数据的分布，稳定地学习到一些浅层的、鲁棒的特征。等模型对数据有了一定的"感觉"后，再增大学习率进行快速优化，效果会更好。

如何评估预热步数

设定预热步数的核心原则是：确保在学习率达到其最大值时，模型的训练已经进入了一个相对稳定的状态。

太短的预热：学习率很快就上升到最大值，此时模型可能还没来得及"适应"数据，依然处于非常不稳定的状态。这可能会导致训练初期的损失出现剧烈震荡甚至不收敛，预热的效果大打折扣。
太长的预热：模型在很长一段时间内都使用非常小的学习率进行训练，收敛速度过慢，浪费了大量的计算资源和时间。

我们的目标就是在这两者之间找到一个平衡点。

前人经验

在实践中，预热步数通常有两种设定方式：

1. 按训练总步数的比例设定：这是最常用、也最推荐的一种方法。它将预热阶段的长度与整个训练过程的长度动态地关联起来。

经验法则：通常将 总训练步数的 6% - 10% 作为预热步数。
为什么有效：这个比例确保了无论你的总训练时间是长是短，预热都只占其中一小部分，既能起到稳定作用，又不会拖慢整体进度。例如，如果你计划总共训练 100,000 步，那么设置 6,000 到 10,000步的预热是一个非常合理的起点。
适用场景：非常适合训练大型模型（如 BERT, GPT）或在大型数据集上从头开始训练。

2. 按固定的周期数（Epochs）设定：对于某些数据集和训练流程，按 Epoch 设定更为直观。

经验法则：通常设置为 1 到 2 个 Epoch。
为什么有效：一个 Epoch 意味着模型已经完整地看过一遍所有训练数据。经过一轮完整的“阅览”，模型通常已经初步适应了数据分布，此时再提升到最大学习率是比较安全的。
适用场景：当数据集不是特别巨大，或者在进行微调（Fine-tuning）任务时，这种方法简单有效。

实践是检验真理的唯一标准

当然，上述 2 个方案都是经验值，最好的方法还是通过实验来验证 —— 评估预热步数是否合适的最佳指标就是 训练初期的损失曲线 (Loss Curve)。

选择一个基准值：根据上面的经验法则，选择一个起始值。例如，如果你在微调一个 BERT 模型，可以先尝试 1 epoch 的预热。
观察损失曲线：开始训练，并密切关注训练日志中前几个 Epoch 的损失变化。
- 理想的曲线：在预热阶段，损失平稳下降。预热结束后，学习率达到最大值，损失开始加速下降，整个过程平滑过渡，没有出现剧烈的尖峰或抖动。
- 预热可能过短的迹象：预热结束后，损失突然出现一个明显的 尖峰 (Spike)，或者开始剧烈震荡，然后才慢慢恢复下降。这说明学习率增长过快，模型没能平稳过渡。
- 预热可能过长的迹象：损失曲线在开始的相当长一段时间内下降得极为缓慢，几乎是一条平线。这说明模型在用一个过小的学习率“浪费时间”。
调整并对比：
- 如果发现损失有尖峰，增加预热步数（例如从 1 epoch 增加到 2 epochs）。
- 如果发现初始收敛太慢，可以尝试减少预热步数。

通过几次短时间的实验（不需要跑完整个训练，观察前几个 epoch 即可），你就能很快地为你的特定任务找到一个合适的预热步数范围。

场景	推荐的起始策略	评估方法
大型模型从头训练 (e.g., GPT, BERT on large corpus)	将总训练步数的 10% 作为预热步数。	观察损失曲线是否平滑，没有尖峰。
中小型模型的微调 (e.g., Fine-tuning ResNet on a custom dataset)	1 到 2 个 Epoch 对应的步数。	观察损失曲线，确保预热结束后能快速收敛。
不确定如何选择时	从 1 个 Epoch 开始，这通常是一个安全且不会太慢的选择。	通过短时实验，观察损失曲线并进行微调。

余弦衰减 (Cosine Annealing)

结论先行

一种学习率的衰减策略。它不像传统的步进式衰减（Step Decay，例如每 30 个 epoch 学习率乘以 0.1）那样是跳崖式下降，而是让学习率随着训练的进行，像余弦函数 cos(x) 在 [0, π/2] 区间一样，平滑地从初始值下降到接近 0。

本质是什么

当模型训练进入中后期，我们通常需要降低学习率，帮助模型在最优点附近进行更精细的搜索。传统的步进式衰减虽然有效，但其"跳崖式"的下降方式有时过于粗暴。

余弦衰减提供了一种更优雅的方案。它让学习率随着训练的进行，像余弦函数一样平滑地从初始值下降到接近 0。

它的本质是：一种 "先探索，后精调" 的动态调整策略。

前期/中期：学习率下降缓慢，保持相对较高的值，让模型有能力跳出局部陷阱，探索更广阔的空间。
后期：学习率下降加速，让模型能以更小的步长在最优解附近精细微调。

这就像飞机降落。飞行员不会在到达目的地后直接关闭引擎（步进衰减），而是会沿着平滑的下滑曲线（余弦曲线）逐渐降低速度和高度，最终实现平稳着陆。

好处有哪些

避免在接近最优点时来回震荡：在训练后期，模型已经非常接近最优解。此时如果学习率依然较大，可能会导致模型在最优解附近来回跳动，始终无法精确收敛。余弦衰减通过缓慢、平滑地降低学习率，使得模型能够以更小的步长，更精细地在最优点附近进行搜索，从而更容易找到那个谷底。
在较长时间内维持相对较大的学习率：与步进式衰减相比，余弦衰减在前期和中期下降得更慢。这意味着模型有更长的时间在损失空间中进行探索，这有助于它跳出一些不好的局部最优解（saddle points or poor local minima），去寻找一个更好的解。

梯度裁剪 (Gradient Clipping)

结论先行

在进行梯度下降更新权重之前，设定一个梯度的阈值。如果当前计算出的梯度向量的 L2 范数（可以理解为梯度的"长度"或"大小"）超过了这个阈值，就按比例缩小这个梯度向量，使其范数恰好等于该阈值。

$$ ||g|| > : \ g g

其中 $g$ 是梯度向量，$||g||$ 是它的 L2 范数，也称为欧几里得范数 (Euclidean Norm)，公式如下：

\[ ||\vec{x}||_2 = \sqrt{x_1^2 + x_2^2 + \dots + x_n^2} \]

本质是什么

在深度网络（尤其是 RNN, Transformer）中，梯度在反向传播过程中可能会因为连乘效应而变得异常巨大，这就是 梯度爆炸 (Exploding Gradients)。一次梯度爆炸带来的权重更新可能是毁灭性的，它会瞬间摧毁模型学到的所有知识，导致损失变为 NaN。

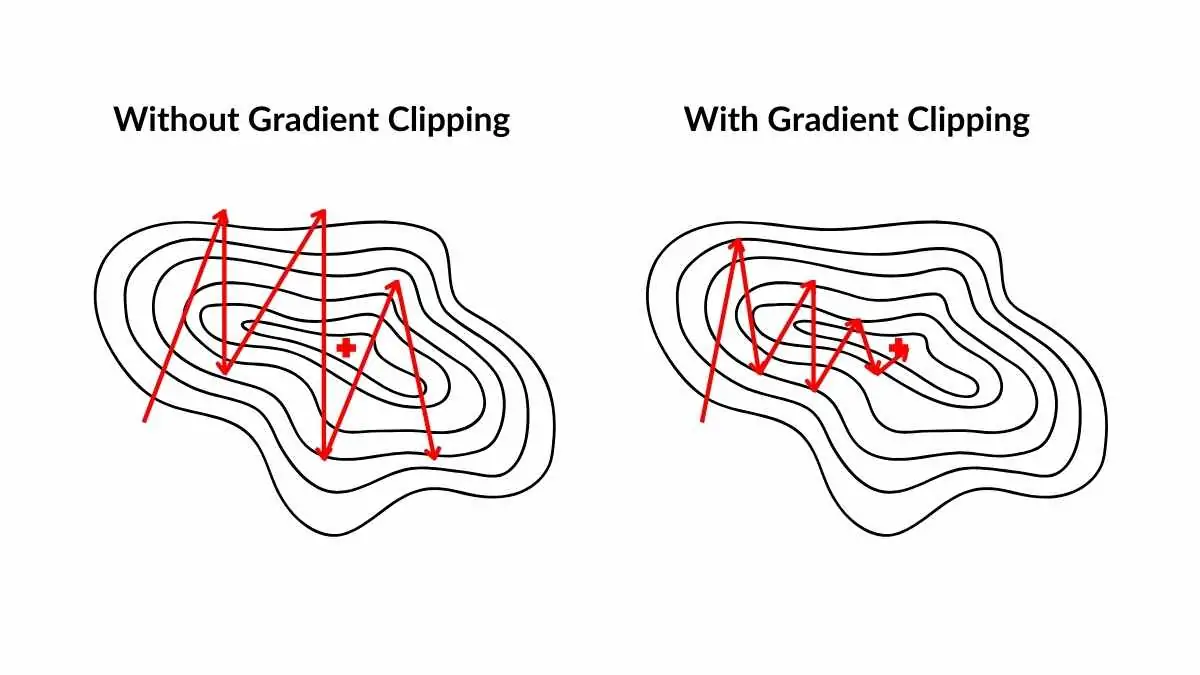
梯度裁剪 (Gradient Clipping) 就是防止这种灾难的"安全带"。它为梯度的大小设定一个上限，如果某次计算出的梯度超过了这个上限，就将其按比例缩小，但 保持其方向不变。

它的本质是：为训练过程增加一个安全约束，牺牲极端情况下的理论最优更新，换取整个训练过程的稳定性和鲁棒性。

有什么好处

这个问题的核心在于 长距离依赖 (Long-term Dependencies) 和 深度（层数）。

在像 RNN 或 Transformer 这样的模型中，信息需要在很长的时间步或很深的层级之间传递。在反向传播计算梯度时，根据链式法则，梯度会涉及到一系列雅可比矩阵（Jacobian Matrix）的连乘。

\[ \frac{\partial L}{\partial h_t} = \frac{\partial L}{\partial h_{t+k}} \cdot \frac{\partial h_{t+k}}{\partial h_{t+k-1}} \cdots \frac{\partial h_{t+1}}{\partial h_t} \]

如果这些矩阵的范数持续大于 1，那么连乘的结果就会呈指数级增长，导致梯度爆炸。
如果持续小于 1，则会导致梯度消失。

梯度裁剪正是为了处理前一种情况。RNN 因为在时间维度上共享权重，这种连乘效应尤其显著。Transformer 虽然没有时间上的循环，但其非常深的网络结构（例如，一个接一个的 self-attention 和 FFN block）同样会形成很长的计算路径，使得梯度在反向传播时也容易出现爆炸或消失的问题。

梯度裁剪通过设定一个上限，确保单次更新的步长不会过大，从而防止了这种灾难性事件的发生。

裁剪方式

前面我们的描述中默认的裁剪方式是：范数裁剪 (Clipping by Norm)，这也是最常用、最推荐的方式。但其实还有另一种方式，叫做值裁剪（Clipping by Value）。理解它们的区别非常重要。

范数裁剪 (Clipping by Norm)

1	torch.nn.utils.clip_grad_norm_(model.parameters(), max_norm=1.0)

计算所有参数梯度的 L2 范数（可以理解为整个梯度向量的“长度”），如果这个范数超过了设定的阈值 max_norm，就将整个梯度向量按比例缩小，使其范数恰好等于 max_norm。

这种裁剪保持梯度的方向不变，只缩放其大小。这非常重要，因为梯度的方向指明了损失函数下降最快的方向，我们希望保留这个正确的信息，只是不想让步子迈得太大。

值裁剪 (Clipping by Value)

1	torch.nn.utils.clip_grad_value_(model.parameters(), clip_value=1.0)

为梯度的每一个元素设定一个区间的 [min_value, max_value]。然后遍历梯度向量中的每一个元素，如果某个元素的值小于 min_value，就把它设为 min_value；如果大于 max_value，就把它设为 max_value。

这种方法会 改变梯度的方向。想象一个二维梯度向量 g = [10, 0.1]，如果设置裁剪区间为 [-1, 1]，裁剪后它会变成 g' = [1, 0.1]。原来的方向几乎是沿着 x 轴，但裁剪后的方向明显向 y 轴偏移了。这种方向上的改变可能会误导模型的更新。

由于范数裁剪保留了梯度的正确方向，在绝大多数情况下，范数裁剪是比值裁剪更好的选择。我们通常所说的梯度裁剪也默认是指范数裁剪。

如何选择裁剪阈值

在上述范数裁剪（后续梯度裁剪均默认为范数裁剪）的示例代码中：

1	torch.nn.utils.clip_grad_norm_(model.parameters(), max_norm=1.0)

max_norm 是一个超参数，即裁剪阈值，它的设定没有一个放之四海而皆准的黄金数值，但有一个非常有效的经验法则来确定它：

初始阶段不裁剪：在你的模型和数据集上，先跑几个训练迭代（iterations），但暂时不使用梯度裁剪。
监控梯度范数：在每个训练步（loss.backward() 之后，optimizer.step() 之前），计算并记录下模型参数的梯度总范数。
分析范数分布：收集上百个迭代的梯度范数值，观察它们的分布。你会发现，大部分时候梯度范数会处在一个比较稳定的范围内，但偶尔会出现一些非常大的"尖峰"，这些就是梯度爆炸的时刻。
设定阈值：选择一个比大多数"稳定"梯度范数略大，但又能明显限制住那些"尖峰"的值。通常可以选择梯度范数分布的某个高百分位点，比如 90% 或 95% 分位点，作为一个不错的起始值。

例如：你观察到 95% 的梯度范数都在 0.5 到 5.0 之间，但偶尔会飙升到 50 或 100。那么，将 max_norm 设置为 5.0 或者 10.0 就是一个合理的选择。这样既不会影响正常的训练，又能有效防止极端情况下的训练崩溃。常见的 max_norm 值通常在 1.0 到 10.0 之间。

在 PyTorch 中，梯度裁剪的位置非常关键。它必须在 loss.backward() 之后（此时梯度已经被计算出来）和 optimizer.step() 之前（在用梯度更新权重之前）调用。

# 一个标准的训练循环
optimizer.zero_grad()        # 1. 清空旧梯度

loss = model(inputs, labels) # 2. 前向传播计算损失
loss.backward()              # 3. 反向传播计算梯度

# --- 梯度裁剪发生在这里 ---
torch.nn.utils.clip_grad_norm_(model.parameters(), max_norm=1.0) # 4. 裁剪梯度

optimizer.step()             # 5. 使用裁剪后的梯度更新权重

代码案例

接下来我们以一个完整的大语言模型（Large Language Model）训练过程，来将这 3 个优化思路串起来，本篇案例参考了 LLMs-from-scratch，感兴趣的读者可参阅此书。

def train_model(model, train_loader, val_loader, optimizer, device,
                num_epochs, eval_freq, eval_iter, start_context, tokenizer,
                warmup_steps, initial_lr=3e-05, min_lr=1e-6):
    train_losses, val_losses, track_tokens_seen, track_lrs = [], [], [], []
    tokens_seen, global_step = 0, -1

    peak_lr = optimizer.param_groups[0]["lr"]
    total_training_steps = len(train_loader) * num_epochs # 计算训练过程中的所有迭代步数
    lr_increment = (peak_lr - initial_lr) / warmup_steps  # 计算在预热阶段学习率的增量

    for epoch in range(num_epochs):
        model.train()
        for input_batch, target_batch in train_loader:
            global_step +=1

            if global_step < warmup_steps:
                lr = initial_lr + global_step * lr_increment    # <---- 学习率预热阶段
            else:
                progress = ((global_step - warmup_steps) /
                                    (total_training_steps - warmup_steps))
                lr = min_lr + (peak_lr - min_lr) * 0.5 * (      # <---- 余弦衰减阶段
                    1 + math.cos(math.pi * progress))
            for param_group in optimizer.param_groups:  # 在优化器上应用计算后的学习率
                param_group["lr"] = lr
            track_lrs.append(lr)

            optimizer.zero_grad()  # 清空旧梯度
            loss = calc_loss_batch(input_batch, target_batch, model, device) # 前向传播计算交叉熵损失
            loss.backward() # 反向传播计算梯度
            if global_step >= warmup_steps: # <--- 在预热阶段后使用梯度裁剪来避免梯度爆炸
                torch.nn.utils.clip_grad_norm_(
                    model.parameters(), max_norm=1.0
                )
            optimizer.step() # 使用裁剪后的梯度更新权重

            tokens_seen += input_batch.numel()

            # 输出调试信息，用于观测训练进展
            if global_step % eval_freq == 0:
                train_loss, val_loss = evaluate_model(
                    model, train_loader, val_loader, device, eval_iter
                )
                train_losses.append(train_loss)
                val_losses.append(val_loss)
                track_tokens_seen.append(tokens_seen)
                print(f"Ep {epoch+1} (Step {global_step:06d}):"
                    f"Train loss {train_loss:.3f}, "
                    f"Val loss {val_loss:.3f}")

        # 运用当前模型进行文本生成，观察模型能力
        generate_and_print_sample(model, tokenizer, device, start_context)
    return train_losses, val_losses, track_tokens_seen, track_lrs

完整代码可参考：llm-from-scratch

总结

深度学习模型的训练过程如同一场充满挑战的远航，不稳定的开局、难以收敛的困境和突如其来的训练崩溃是常见的"风浪"。本文深入探讨了三种为这场远航保驾护航的核心技巧：

学习率预热 (Learning Rate Warmup)：它确保了我们能有一个"温柔的启动"，通过在训练初期使用极小的学习率并逐步提升，有效避免了因模型尚未适应数据而导致的剧烈震荡。
余弦衰减 (Cosine Annealing)：它为我们规划了"平滑的航程"，以一种先慢后快的方式优雅地降低学习率，兼顾了前中期的广泛探索和后期的精细收敛，帮助模型更精准地抵达最优解。
梯度裁剪 (Gradient Clipping)：它是全程必备的"安全带"，通过为梯度设置上限，有效防止了因梯度爆炸引发的"核爆"事故，保证了训练过程的稳定和鲁棒。

文章最后的代码示例生动地展示了，这三个技巧并非孤立存在，而是三位一体的协同策略。在一个典型的训练流程中，我们以预热开启，用余弦衰减贯穿全程，并由梯度裁剪时刻守护。

掌握并善用三个优化技巧，将不再是玄学调参，而是有章可循的工程科学，能让你的模型训练过程更加稳定、高效，最终得到更优的性能。

本文采用署名-非商业性使用-相同方式共享 4.0 国际许可协议，转载请注明出处。

模型训练核心技巧：学习率预热、余弦衰减与梯度裁剪

学习率预热 (Learning Rate Warmup)

结论先行

本质是什么

好处有哪些

如何评估预热步数

前人经验

实践是检验真理的唯一标准

推荐方案

余弦衰减 (Cosine Annealing)

结论先行

本质是什么

好处有哪些

梯度裁剪 (Gradient Clipping)

结论先行

本质是什么

有什么好处

裁剪方式

如何选择裁剪阈值

代码案例

总结