Redis 数据类型丨Sorted Set丨listpack vs. skiplist+dict

在 Redis 的数据世界里，如果说 String 是基石，Hash 是对象的映射，那么 Sorted Set (ZSet) 则是那个将排序与集合两大特性完美融合的瑞士军刀。它不仅能胜任各种排行榜系统，还能在延迟队列、范围查找等高级场景中大放异彩。

然而，你是否想过：

• 为什么 ZADD 一个新成员的时间复杂度是 \(O(logN)\)？
• 为什么 Redis 既需要一个哈希表 (dict) 又需要一个跳表 (skiplist) 来实现它？
• 在什么情况下，它又会变身为一种叫做 listpack 的紧凑结构？

今天，就让我们从第一性原理出发，穿透 API 的表象，直抵 Sorted Set 的设计核心，彻底理解它在性能与内存之间的极致平衡。

Sorted Set 要解决的核心矛盾

任何精妙设计的背后，都是为了解决一个根本性的矛盾。Sorted Set 要解决的核心矛盾是：如何创建一个既能通过成员（member）快速查找、又能根据分数（score）高效排序和范围查找的数据集合？

让我们来推演一下：

1. 如果只有"集合"需求：我们需要一个能存储唯一成员并能 \(O(1)\) 快速查找的数据结构。毫无疑问，哈希表 (Hash Table / Dictionary) 是最佳选择。但它的致命弱点是——无序。
2. 如果只有"排序"需求：我们可以用有序数组或平衡二叉搜索树。
   • 有序数组：范围查找性能极佳（二分法），但插入和删除的成本太高 (\(O(N)\))，因为需要移动大量元素。
   • 平衡二叉搜索树（如红黑树）：插入、删除、查找都是 \(O(logN)\)，性能很好。但实现非常复杂，且在范围查找上不如跳表直观。

可以看到，单一的数据结构无法同时满足"集合"和"排序"两大需求。因此，Redis 必须采用一种复合型的设计。这正是 Sorted Set 内部"双引擎"模式的理论基础。

揭秘 Sorted Set 的内部编码

为了在不同场景下都达到最优的性能与内存平衡，Redis 为 Sorted Set 提供了两种内部编码（Encoding），对用户透明，但内部会自动转换。

1. listpack：极致紧凑的"数组"模式

当 Sorted Set 中存储的元素数量很少，并且每个元素的值都不大时，Redis 会选择 listpack 编码。

• 触发条件 (redis.conf 默认配置):
  • 元素数量小于 zset-max-listpack-entries 128
  • 所有元素值的字节长度小于 zset-max-listpack-value 64
• 底层原理：listpack 本质上是一块连续的内存空间，它将每个 (member, score) 对紧凑地序列化存储。为了保持有序，每次插入都需要找到正确的位置，这可能导致其后的数据发生移动。
• 性能权衡:
  • 优点：内存利用率极高，因为它消除了所有指针开销。
  • 缺点：插入、删除、查找的时间复杂度都是 \(O(N)\)。
  • 设计哲学：这是一种典型的用时间换空间的策略。当 N 非常小（例如小于128）时，\(O(N)\) 的操作成本极低，几乎是瞬时的，而节省下来的内存却非常可观。

关于 listpack 的具体说明，可以参考之前的Redis 数据类型丨List丨从双向链表到 Listpack 的演进之路 (基于 Redis 8.2.1 源码)，它们其实是一个东西！

2. skiplist + dict：高性能"双引擎"模式

一旦 listpack 的任一触发条件被打破，Redis 会自动将其转换为 skiplist + dict 编码。这才是 Sorted Set 的完全体形态。

• dict (字典/哈希表)：负责"集合"的部分。它建立了一个从 member 到 score 的映射。这使得 ZSCORE 这种通过成员获取分数的操作，时间复杂度是完美的 \(O(1)\)。
• zskiplist (跳表)：负责"排序"的部分。它将所有的 (score, member) 对按照 score（分数相同则按 member 字典序）进行排序。跳表的特性使得插入、删除和按排名/分数范围查找的平均时间复杂度都是 \(O(logN)\)。

数据共享：为了节约内存，dict 和 skiplist 中的 member 字符串是共享的，即它们都指向同一个 SDS (Simple Dynamic String) 对象。

跳表的核心思想是空间换时间和随机化。

想象一下，一个普通的单链表，查找效率是 \(O(N)\)。现在，我们从这个链表中，随机抽取一些节点，给它们增加一个"上层指针"，指向下一个被抽取的节点。这样我们就构建了第 2 层"快速通道"。我们可以不断重复这个过程，构建出多层快速通道。

当我们要查找一个元素时：

1. 从最高层的"快速通道"开始。
2. 在当前层向右查找，直到找到的下一个节点比目标大，或者到了链表末尾。
3. 然后从当前节点下降一层，重复步骤 2。
4. 最终在最底层（原始链表）找到目标位置。

因为高层索引可以让你"跳过"大量节点，所以平均查找效率被提升到了 \(O(logN)\)。而这种层级的建立是完全随机的，它通过概率来维持整体的平衡，避免了红黑树那样复杂的平衡操作。

这就是 Redis 选择跳表的原因：用更简单的实现，达到了与平衡树相媲美的性能。

数据结构与核心算法

理解了顶层设计，我们深入到 Redis 的 C 源码，看看这些结构是如何定义的，在 Redis 8.2.1 的源码中，关于 zset 的类型定义位于 server.h 文件中。如下所示，它主要包含 3 个核心数据结构：zset、zskiplist 和 zskiplistNode。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

/* Sorted Set 整体结构 */
typedef struct zset {
    dict *dict;         // 哈希表，实现 member -> score 的 O(1) 查找
    zskiplist *zsl;     // 跳表，实现排序与范围查找
} zset;

/* 跳表结构 */
typedef struct zskiplist {
    struct zskiplistNode *header, *tail; // 头、尾节点
    unsigned long length;                 // 节点数量
    int level;                            // 当前最大层数
} zskiplist;

/* 跳表节点结构 */
typedef struct zskiplistNode {
    sds ele;                          // 成员 (member)
    double score;                     // 分数 (score)
    struct zskiplistNode *backward;   // 后退指针 (仅在 L0 层)
    struct zskiplistLevel {
        struct zskiplistNode *forward; // 前进指针
        unsigned long span;            // 跨度 (到下一个节点的距离)
    } level[];                        // 柔性数组，存储每一层的信息
} zskiplistNode;

从比较直观的角度来讲的话，跳表的结构可以用下图来演示：

如果要完全复刻上述所定义出来的数据结构，那表示起来可能会有点复杂，这里我画了张图，供你参考：

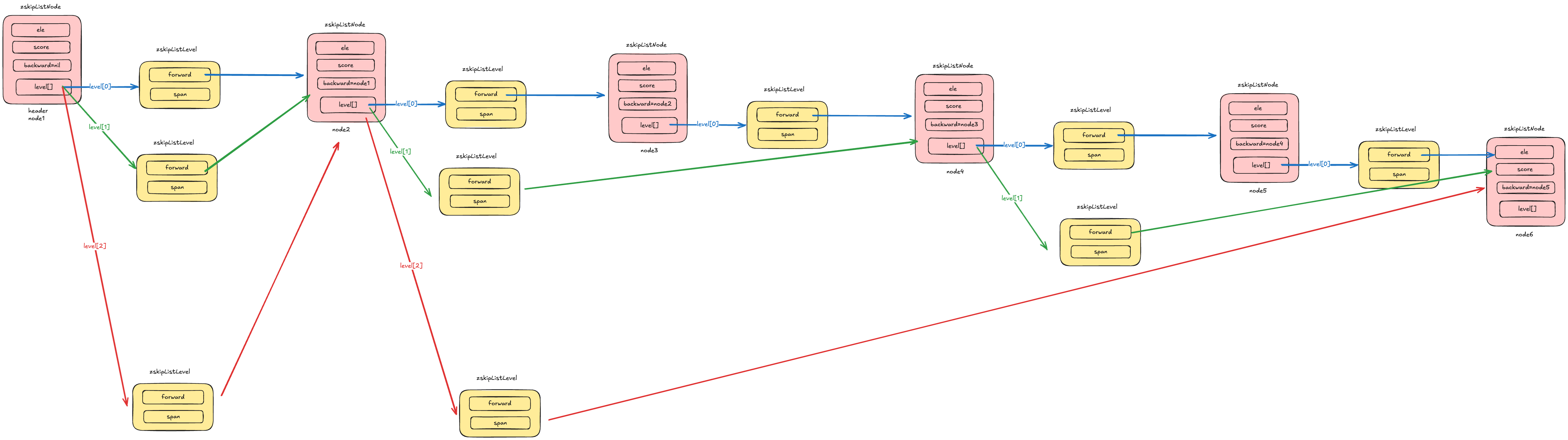
接下来我们从一个最核心的插入逻辑来更进一步了解跳表的实现细节。 zset 的核心实现逻辑位于 t_zset.c 文件中，其中插入操作由 zslInsert 函数来实现。这里我先把完整的代码和注释给你，接下来我们再一一拆解。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86

/* Insert a new node in the skiplist. Assumes the element does not already
 * exist (up to the caller to enforce that). The skiplist takes ownership
 * of the passed SDS string 'ele'. */
zskiplistNode *zslInsert(zskiplist *zsl, double score, sds ele) {
    // update: 记录新节点在每一层的前驱节点（需要被更新的节点）
    // rank:   记录从 header 到每一层前驱节点时，跨越了多少个节点
    zskiplistNode *update[ZSKIPLIST_MAXLEVEL], *x;
    unsigned long rank[ZSKIPLIST_MAXLEVEL];
    int i, level;

    serverAssert(!isnan(score));
    x = zsl->header; // 从跳表的头节点开始

    /* 1. 侦察与降落：从顶层向下查找插入位置 */
    // 从跳表现有的最高层开始，逐层下降
    for (i = zsl->level-1; i >= 0; i--) {
        // rank[i] 继承了上一层（i+1）的排名。
        // 如果是最高层，初始排名为 0。
        rank[i] = i == (zsl->level-1) ? 0 : rank[i+1];

        // 在当前层向右前进，直到下一个节点的分数大于目标分数，
        // 或者分数相同但元素的字典序大于目标元素。
        while (x->level[i].forward &&
               (x->level[i].forward->score < score ||
                   (x->level[i].forward->score == score &&
                    sdscmp(x->level[i].forward->ele,ele) < 0)))
        {
            // 每跨越一个节点，就将该节点的跨度(span)累加到排名中
            rank[i] += x->level[i].span;
            x = x->level[i].forward; // 前进到下一个节点
        }
        // 找到了！x 是新节点在第 i 层的前驱节点。记录下来。
        update[i] = x;
    }

    /* 2. 随机决定新节点的层数 */
    // zslRandomLevel() 通过一个概率算法（幂次定律）返回一个随机的层数。
    // 大部分节点的层数很低（如1），极少数节点的层数会很高。
    level = zslRandomLevel();

    // 如果随机出的层数比当前跳表的最高层还高
    if (level > zsl->level) {
        // 为新的、更高的层级初始化 update[] 和 rank[]
        for (i = zsl->level; i < level; i++) {
            rank[i] = 0;
            update[i] = zsl->header;
            // 在新层级，header 的跨度是整个跳表的长度
            update[i]->level[i].span = zsl->length;
        }
        zsl->level = level; // 更新跳表的总层数
    }

    /* 3. 创建新节点，并进行“穿针引线”般的链接操作 */
    x = zslCreateNode(level,score,ele);
    for (i = 0; i < level; i++) {
        // a. 链接 forward 指针
        // 将新节点的 forward 指针指向其前驱节点原来的下一个节点
        x->level[i].forward = update[i]->level[i].forward;
        // 将前驱节点的 forward 指针指向新节点
        update[i]->level[i].forward = x;

        // b. 更新 span（跨度），这是 ZRANK 命令能实现 O(logN) 的关键
        // 新节点的 span = 前驱节点原来的 span - (从前驱节点到插入位置的距离)
        x->level[i].span = update[i]->level[i].span - (rank[0] - rank[i]);
        // 前驱节点的 span = (从前驱节点到插入位置的距离) + 1
        update[i]->level[i].span = (rank[0] - rank[i]) + 1;
    }

    /* 4. 更新未被触及的高层级的 span */
    // 对于那些高于新节点层数的层级，新节点并未插入其中。
    // 但因为跳表总长度增加了1，所以这些层级中，新节点前驱节点的 span 需要加 1。
    for (i = level; i < zsl->level; i++) {
        update[i]->level[i].span++;
    }

    /* 5. 更新 backward 指针（双向链表部分） */
    // backward 指针只存在于最底层（level 0），用于 ZREVRANGE 等反向遍历命令
    x->backward = (update[0] == zsl->header) ? NULL : update[0];
    if (x->level[0].forward)
        x->level[0].forward->backward = x;
    else
        zsl->tail = x; // 如果新节点是最后一个节点，更新跳表的 tail 指针

    zsl->length++; // 跳表总长度加 1
    return x;
}

zslInsert 的整个过程，可以比喻为一次精准的空降行动：

1. 侦察：从最高空（顶层索引）开始，确定空降的大致区域。
2. 降落：逐层下降，不断修正位置，最终在地面（最底层）找到精准的着陆点。
3. 建设：建立新的节点，并将其接入到各个层级的交通网络中。

更具体来说，其过程可以分解为以下几个步骤：

1. 路径记录：创建一个 update[] 数组。从跳表的最高层开始，逐层向右查找，直到找到新节点应插入的位置。将每一层"降落"前的最后一个节点记录在 update[] 数组中，形成一条插入路径。同时，rank[] 数组记录路径上跨越的节点总数，用于后续更新 span。
2. 随机层高 ：为新节点随机生成一个层数 (level)。这是跳表维持平衡和 O(logN) 性能的关键，它通过概率论避免了平衡树复杂的旋转操作。
3. 节点链接：创建新节点，并利用 update[] 数组中记录的路径，在 0 到 level-1 的每一层中，像操作链表一样，将新节点精准地插入到前驱和后继节点之间。
4. 跨度更新：这是 ZRANK 等排名命令能实现 \(O(logN)\) 的精髓。在链接节点的同时，精确地更新 update[] 路径上所有节点的 span 值以及新节点自身的 span 值。

接下来我们来一一拆解这段代码的每一个细节。

第 1 步：初始化与准备

1
2
3
4
5
6

zskiplistNode *zslInsert(zskiplist *zsl, double score, sds ele) {
    // update: 记录新节点在每一层的前驱节点（需要被更新的节点）
    // rank:   记录从 header 到每一层前驱节点时，跨越了多少个节点
    zskiplistNode *update[ZSKIPLIST_MAXLEVEL], *x;
    unsigned long rank[ZSKIPLIST_MAXLEVEL];
    int i, level;

• zskiplistNode *update[ZSKIPLIST_MAXLEVEL]: 路径记录仪。它是一个指针数组，update[i] 将用于存储新节点在第 i 层的前驱节点。为什么需要它？因为插入操作的本质就是在 update[i] 和它原来的下一个节点之间，插入我们的新节点。这个数组为我们保存了所有需要修改的连接点。
• unsigned long rank[ZSKIPLIST_MAXLEVEL]: 距离计数器。rank[i] 用于记录从跳表 header 头节点出发，到达 update[i] 这个节点时，在最底层（第 0 层）总共跨越了多少个节点。它的核心作用是为后续精确计算和更新节点的 span（跨度）提供数据支持，这是 ZRANK 命令能够实现 \(O(logN)\) 的基石。

第 2 步：查找插入位置并记录路径

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

x = zsl->header; // 从跳表的头节点开始

// 从跳表现有的最高层开始，逐层下降
for (i = zsl->level-1; i >= 0; i--) {
    // rank[i] 继承了上一层（i+1）的排名。
    rank[i] = i == (zsl->level-1) ? 0 : rank[i+1];

    // 在当前层向右前进
    while (x->level[i].forward &&
           (x->level[i].forward->score < score ||
               (x->level[i].forward->score == score &&
                sdscmp(x->level[i].forward->ele,ele) < 0)))
    {
        // 每跨越一个节点，就将该节点的跨度(span)累加到排名中
        rank[i] += x->level[i].span;
        x = x->level[i].forward; // 前进到下一个节点
    }
    // 记录第 i 层的前驱节点
    update[i] = x;
}

这是跳表算法的精髓所在——分层查找。

• for (i = zsl->level-1; i >= 0; i--): 循环从最高层（zsl->level-1）开始，逐层下降到最底层（0）。这模仿了我们在地图上查找位置的过程：先看洲际地图（高层），再看国家地图（中层），最后看城市街道图（底层）。高层级的"快速通道"可以让我们一次性跳过大量节点。
• while (...): 在当前层级，不断向右移动。判断条件 (score < ... || (score == ... && ele < ...)) 保证了跳表的排序规则：优先按 score 升序，如果 score 相同，则按 member 的字典序升序。
• rank[i] += x->level[i].span;: 这是 rank 数组工作的核心。每当我们从 x 节点跳到它的下一个节点时，并不是只前进了一步，而是前进了 x->level[i].span 步。我们将这个跨度累加到 rank[i] 中，rank[i] 就实时记录了我们距离起点的总步数。
• update[i] = x;: 当 while 循环结束时，x 节点就是新节点在第 i 层的前驱节点。我们将其记录在 update[i] 中。当整个 for 循环结束后，update 数组就完整记录了从最高层到最底层的一条插入路径。

第 3 步：确定新节点层高并处理新层级

1
2
3
4
5
6
7
8
9
10

level = zslRandomLevel();

if (level > zsl->level) {
    for (i = zsl->level; i < level; i++) {
        rank[i] = 0;
        update[i] = zsl->header;
        update[i]->level[i].span = zsl->length;
    }
    zsl->level = level;
}

• level = zslRandomLevel(): 概率之美。新节点将拥有几层"快速通道"？这里不是由复杂的平衡算法决定，而是通过一个简单的概率函数随机生成。大部分节点只有 1 层，极少数节点会有很高的层数。正是这种随机性，使得跳表在整体上能够维持一个高效的对数级结构。
• if (level > zsl->level): 处理一个特殊情况。如果随机出的 level 比当前跳表的最大层数还大，意味着我们需要为整个跳表加盖新的楼层。在这些新楼层，路径上的前驱节点自然就是 header 节点，并且它到 NULL 的跨度就是整个跳表的长度 zsl->length。

第 4 步：节点创建、链接与跨度更新

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

x = zslCreateNode(level,score,ele);
for (i = 0; i < level; i++) {
    // a. 链接 forward 指针
    x->level[i].forward = update[i]->level[i].forward;
    update[i]->level[i].forward = x;

    // b. 更新 span（跨度）
    x->level[i].span = update[i]->level[i].span - (rank[0] - rank[i]);
    update[i]->level[i].span = (rank[0] - rank[i]) + 1;
}

// c. 更新高层及跨度
for (i = level; i < zsl->level; i++) {
    update[i]->level[i].span++;
}

这是整个插入过程中最核心的逻辑：

• 链接 forward 指针: 这两行是经典的链表插入操作。假设原来是 A -> C，A 就是 update[i]，C 就是 update[i]->level[i].forward。现在，我们将新节点 x 插入其中，变为 A -> x -> C。

• 更新 span (跨度): 这是最精妙的部分，我们用一个例子来说明。

  • 假设在第 i 层，前驱节点 A (即 update[i]) 原来的 span 是 10，它直接指向 C。
  • 我们在第 0 层（最底层）的查找过程中，从 A 之后，又前进了 3 步才找到插入点。这意味着 rank[0] - rank[i] 的值是 3（可以理解为 A 在高层和底层之间的投影偏差）。
  • update[i]->level[i].span = (rank[0] - rank[i]) + 1;: A 的新 span 变为 3 + 1 = 4。因为它现在指向新节点 x，它俩之间跨越了 3 个旧节点，加上 x 本身，总共是 4 步。
  • x->level[i].span = update[i]->level[i].span - (rank[0] - rank[i]);: 新节点 x 的 span 等于 A 的旧 span (10) 减去它俩之间的距离 (3)，等于 7。

  验证: 插入后，A 的新 span (4) + x 的新 span (7) = 11。而 A 的旧 span 是 10。总跨度增加了 1，正好等于新加入的节点数量。完美！

另外，对于那些高于新节点 level 的层级，新节点并不会被插入。但是，由于整个跳表的总长度增加了 1，这些更高层级上、位于插入路径上的前驱节点（update[i]），它们指向的下一个节点的相对距离也增加 1。因此，它们的 span 值需要递增。

第 5 步：更新后退指针和表尾

1
2
3
4
5
6
7

x->backward = (update[0] == zsl->header) ? NULL : update[0];
if (x->level[0].forward)
    x->level[0].forward->backward = x;
else
    zsl->tail = x;

zsl->length++;

最后的收尾工作。

• x->backward = ...: 跳表的最底层（level[0]）是一个双向链表，backward 指针用于支持 ZREVRANGE 等反向遍历命令。这里将新节点的后退指针正确地指向它的前驱节点 update[0]。
• if...else...: 更新新节点的后继节点的 backward 指针，让它指向新节点 x。如果新节点是最后一个节点，则更新整个跳表的 tail 指针。
• zsl->length++: 最后，将跳表的总长度加 1。

至此，一个新节点被天衣无缝地织入了跳表这张大网中，所有相关的指针和跨度信息都得到了原子性的更新。

Sorted Set 的典型应用场景

理论的价值在于实践。Sorted Set 的强大能力使其在众多业务场景中成为关键先生。

1. 排行榜

这是最经典的应用。例如，游戏玩家积分榜、文章点赞榜。

• 更新排名：ZADD leaderboard 100 user1 (分数变化时，再次 ZADD 即可覆盖)
• 获取 Top 10：ZREVRANGE leaderboard 0 9 WITHSCORES
• 查询我的排名：ZREVRANK leaderboard user1 (返回从 0 开始的排名)

2. 延迟消息队列

一个非常巧妙且实用的高级用法。

• 生产者：将消息的执行时间（timestamp）作为 score，消息内容作为 member，添加到 ZSet 中。

  1	ZADD delay_queue 1758153600 '{"job_id": 123, "task": "send_email"}'

• 消费者：定期轮询 ZSet，取出 score 小于等于当前时间的任务。

  1	ZRANGEBYSCORE delay_queue -inf (current_timestamp) LIMIT 0 1

  如果拉取成功，立即用 ZREM 将其从队列中删除，防止被其他消费者重复执行。

3. 带权重的自动补全

例如，在搜索框中，根据输入的前缀，推荐出频率更高（权重更高）的词条。

• 数据准备

  1	ZADD autocomplete 100 "redis" 90 "reids" 80 "reload"

• 查询实现：利用 ZRANGEBYLEX 命令查找所有以 "re" 开头的词条

  1	ZRANGEBYLEX autocomplete "[re" "[re\xff"

命令速查表

总结

Sorted Set 是 Redis 中设计最为精巧的数据结构之一。它深刻体现了计算机科学中的权衡（Trade-off）思想。

• 通过listpack 与 skiplist+dict 的双编码策略，它在内存占用和执行效率之间找到了动态的平衡点。
• 通过dict 与 skiplist 的双引擎复合结构，它完美地解决了“按成员查找”与“按分数排序”的核心矛盾。

理解了这些底层原理，你将不仅仅是一个 Redis API 的使用者，更能成为一名能够根据场景预判性能、优化结构、将 Redis 的威力发挥到极致的架构师。

许可协议

本文采用 署名-非商业性使用-相同方式共享 4.0 国际 许可协议，转载请注明出处。

分享文章